Encryption, 80 years after the Enigma machine

This year is the 80th anniversary of a pivotal event during World War II: the decoding of the Enigma machine by the Allied forces. Mathematician Alan Turing, among others, played a crucial role in cracking the device used by the Germans for secret military transmissions. This breakthrough not only influenced the course of the war but also drove advancements in cryptography, a field shaped by the perpetual struggle between people trying to securely transmit information and others who try to crack codes and gain access to that information. It’s a struggle that spurs the innovation and development of ever more sophisticated encryption systems.

The first ciphers relied on mono-alphabetic substitution, a simple scheme where each letter of the plain text is replaced with another letter of the alphabet. It uses a fixed key, which consists of the 26 letters of a shuffled alphabet. For example, the letter “e” is changed to “g.” The problem with this system is that the frequency of the letters in the original text persists in the encrypted text. If the encrypted message contains many of the letters “g” and “q,” these probably correspond to some of the most frequent letters in various languages, like “e” and “a.” This led to the technique of frequency analysis in cryptography. The Gold-Bug, a short story by Edgar Allan Poe, explains the technique as the two protagonists try to decipher a secret message that will lead to a buried treasure.

To address this weakness, polyalphabetic substitution ciphers were developed. These ciphers encode letters differently, using multiple substitution rules throughout the text. In classic examples like the Vigenère cipher, each letter of the plain text is encoded with a different cipher, whose increment is determined by the corresponding letter of another text — this is called the key.

Although the Enigma machine used polyalphabetic substitution encryption, it represented a significant advancement compared to classical polyalphabetic techniques. It used an electromechanical rotor mechanism that scrambled the 26 letters of the alphabet. In typical use, one person enters text on the Enigma’s keyboard and another person writes down which of the 26 lights above the keyboard is illuminated at each key press. The illuminated letters are the ciphertext. Entering ciphertext on the keyboard transforms it back into readable text. The intricate rotor mechanism enabled the use of an enormous number of different rules, making it extremely difficult to crack the code, which is only possible if the initial machine configuration is known. But small system issues, combined with several years of hard work, mathematical and computational advancements, and a dose of luck, ultimately cracked the Enigma code.

One weakness of Enigma was the need to distribute machine configuration information (or keys) in advance, which carried the risk of potential interception. The challenge of securely exchanging keys was the next cryptography problem to address for enhanced system resilience. The solution came in the 1970s with the Diffie-Hellman key exchange protocol.

Imagine Alice and Bob wanting to communicate privately without meeting in person. To do this, they need to agree on a secret key. To explain this protocol, let’s use a straightforward analogy: mixing paint colors. Alice and Bob publicly agree on an arbitrary starting color that does not need to be kept secret. In this example, the color is yellow. Each person also selects a secret color that they keep to themselves — in this example, red and cyan. The crucial part of the process is that Alice and Bob each mix their own secret color together with their mutually shared color, resulting in orange-tan and light-blue mixtures respectively, and then publicly exchange the two mixed colors. Finally, each of them mixes the color they received from the partner with their own private color. The result is a final color mixture (yellow-brown in this case) that is identical to their partner’s final color mixture.

If someone intercepts the message, they would only know the common color (yellow) and the first mixed colors (orange-tan and light-blue), but it would be very hard for them to find out the final secret color (yellow-brown).

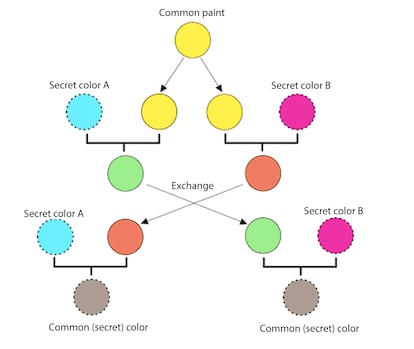
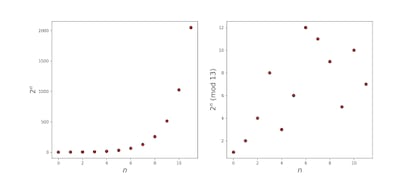
By using large numbers rather than colors, it becomes impossible to decipher in a practical amount of time, even for modern supercomputers. Encryption security is achieved through a fast computer calculation known as modular arithmetic exponentiation. However, it is extremely challenging to reverse engineer the original input based solely on the result. While regular exponentiation follows a predictable pattern, modular arithmetic exponentiation is highly unpredictable and difficult to undo. This is commonly referred to as the discrete logarithm problem.

But before agreeing upon a common key to use, the people communicating need to verify that the other person is not an impostor. This is where digital authentication certificates come in. Once these certificates are exchanged, the Diffie-Hellman method can be used to agree upon a secret key. Finally, the message can be encrypted and sent securely. The processes are more complex than described here, but these fundamental ingredients are essential for secure online communication today. While the field keeps evolving, these protocols have remained completely secure for many years. However, there will always be people who dare to challenge them, keeping the cryptographic battle alive and thriving.

Sign up for our weekly newsletter to get more English-language news coverage from EL PAÍS USA Edition