Cryptography: The math that makes instant messaging secure
The protocol used by WhatsApp employs concepts such as elliptic curves, the elliptic discrete logarithm and modular arithmetic

WhatsApp, the popular instant messaging app, guarantees the security of your messages with an end-to-end encryption system. With this method, in which the encryption and decryption of the messages takes place directly on the user’s phone and where the encryption keys are renewed with each message, it can be ensured that, except for the recipients, no one — not even the app itself — can read the communications. To do this, mathematical concepts such as elliptic curves, the discrete elliptic logarithm and modular arithmetic are used.
The system used by WhatsApp is symmetric; that is, it uses the same key to encrypt and decrypt messages (in contrast, asymmetric systems use different encryption and decryption keys). Symmetric systems require less computing resources and are easier to use, but with them it is essential to guarantee the security of the common key shared by two people. This key is generated by exchanging information over a public channel, using the method introduced by Whitfield Diffie and Martin Hellman in 1976. The challenge lies in designing one-way algorithms (or functions), that is, that they are easy to execute, but that, from the result, it is not computationally possible to find the starting point.
To create a common secret key, each user chooses a number, which will be kept secret; that will be the private key. From it, by means of a one-way function, a public key will be produced. Then, each one does the same calculations on their own, starting from their own private key and the public key of the other user, so that both obtain the same number: that is the common key.
In 1985, Neal Koblitz and Victor Miller independently proposed using Diffie-Hellman methods based on the points of a type of curve known as elliptic. The advantage of this is that the keys are relatively small — only 256 bits — and easy to execute.
WhatsApp uses the Montgomery Curve25519 elliptic curve, introduced by Daniel J. Bernstein in 2005, whose equation is y² = x³ + 486662x² + x.
Mathematical operations are performed in modular arithmetic. Specifically, a sum is defined on the points of the elliptic curve, which is explained in the following image. From it, the “d-times sum” of a point P — known as dP — is determined; this is the unidirectional function that allows obtaining the secure common keys on which the encryption is based.
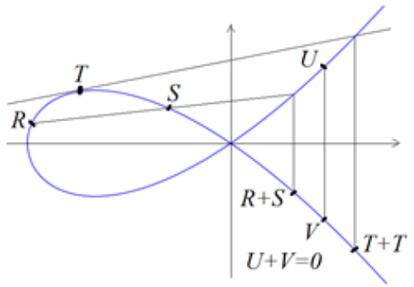
To do this, the two users — let’s call them Ander and Beatriz — choose their secret number; d1 and d2, respectively. Each one calculates their public key by adding the chosen base point P to the times determined by their secret number. Ander’s result is d1P and Beatriz’s is d2P. Next, with his private key and Beatriz’s public key, Ander calculates d1(d2P), while Beatriz calculates d2(d1P). Both get the same result (the dP operation is commutative), which is the common secret key. As we stated earlier, the security of the method lies in guaranteeing that from a dP result it is not possible to computationally obtain the number d that generated it; that is, in that it is a one-way only function. This is known as the elliptic discrete logarithm problem.
Once the common key is available, WhatsApp encrypts and decrypts the messages on the device itself. This is done with the Advanced Encryption Standard symmetric cryptographic system (which is a version of the Rijndael algorithm for 256-bit keys, developed in 1998 by Vincent Rijmen and Joan Daemen). With today’s computing power, it is virtually unbreakable.
WhatsApp users generate and renew, with each message, the common encryption and decryption key, which further increases the reliability of the system. For each batch of messages, the user generates a pair of private-public keys on their phone and, with their private key and the recipient’s public key, calculates the common root key. From it, it automatically generates, in a chained way, a different subkey to encrypt each message. The header of the messages includes the public key. The recipient calculates the same root key, and with it, obtains the subkeys and decrypts the messages. It does the same for their responses, and when the person who started the communication receives them, they renew the private-public keys and replicate the process as many times as necessary. Thus, with each batch of messages, the root key and the message subkeys are renewed.
Other instant messaging apps also use end-to-end encryption to protect all communications, but not all of them work this way. For example, Telegram has an encryption option with its own protocol, called MTProto. With it, instead of saving the messages locally, the app stores them in the cloud.
Mikel Lezaun is a professor of applied mathematics at the University of the Basque Country (UPV/EHU).
Sign up for our weekly newsletter to get more English-language news coverage from EL PAÍS USA Edition
Tu suscripción se está usando en otro dispositivo
¿Quieres añadir otro usuario a tu suscripción?
Si continúas leyendo en este dispositivo, no se podrá leer en el otro.
FlechaTu suscripción se está usando en otro dispositivo y solo puedes acceder a EL PAÍS desde un dispositivo a la vez.
Si quieres compartir tu cuenta, cambia tu suscripción a la modalidad Premium, así podrás añadir otro usuario. Cada uno accederá con su propia cuenta de email, lo que os permitirá personalizar vuestra experiencia en EL PAÍS.
¿Tienes una suscripción de empresa? Accede aquí para contratar más cuentas.
En el caso de no saber quién está usando tu cuenta, te recomendamos cambiar tu contraseña aquí.
Si decides continuar compartiendo tu cuenta, este mensaje se mostrará en tu dispositivo y en el de la otra persona que está usando tu cuenta de forma indefinida, afectando a tu experiencia de lectura. Puedes consultar aquí los términos y condiciones de la suscripción digital.