Knot theory: How many times is it possible to twist a rope on itself?
This branch of topology analyzes the properties of elastic curves that are entangled in space and can be unraveled by manipulating their parts without breaking them

In mathematics we often start with a simple question that leads us down unexpected paths. For example, how many times is it possible to knot a rope on itself? In the real world, various physical constraints determine the answer: the length of the rope, its elastic capacity and thickness. But if we strip the question of all these physical constraints, we are left with a mathematical brainteaser.
A mathematical knot is an elastic curve that is entangled in space and can be unraveled by manipulating its parts without breaking them. Mathematical knots have their ends fused together, like the line that makes a circle. This is the simplest knot, the trivial knot; but it is not the only one.
The diversity of these mathematical entities is infinite and one of the tasks of knot theory, which is an area of topology, is to describe it. To do this, it is necessary to determine when two knots are the same: for example, they will be the same when it is possible to twist one into the other, without breaking it. Hopefully, if they are the same this process ends at some point, but if they are not, we can spend a lot of time without ever reaching an answer.
To save us from going down this path, knot theory takes care of identifying the mathematical properties that can be checked more easily. Of these, the simplest is to count how many times the curve crosses when drawn on a sheet of paper, indicating which part crosses above and which part below.
However, the same knot can have many different representative diagrams, not only according to the point of view from which it is drawn. There could also be some crossings that would disappear simply by twisting some part of the knot slightly.
The minimum number of crossings that can be obtained in a knot diagram tells us if two knots are different; for example, if one has three and the other has four crossings. And it also makes it possible to organize the knots in a large catalog, starting with the simplest: the circle, or trivial knot, which can be drawn without any crossings.
All knots that can be drawn with one or two crossings can be manipulated in such a way that they are identical to a circle. There is only one knot with three crossings and it is known as the trefoil knot – the first non-trivial knot. The figure-eight knot is the only knot that can be drawn with four crossings, but after that number of crossings, there is a sudden increase in diversity. The catalog of knots with up to ten crossings has 250 different knots, and with up to 19, the number rises to more than 300 million.
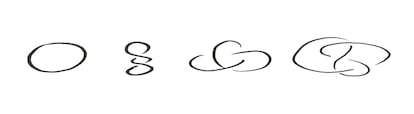
A wild knot has an infinite number of crossings and provides an answer to the question we initially posed. To imagine it, we can use a recipe that, although infinite, is relatively simple. The important ingredient concerns spherical mirrors, which show the reflected image of the whole space on their surface as if it were inside the sphere. The mirror deforms most figures: straight lines are seen as curved and we inevitably think of a fish when looking at our face reflected in it. The only figure that does not change when reflected, apart from its size, is the figure of any other sphere.
This is the key to the recipe because that other sphere could also be made of mirrors and, in that case, if we look carefully we would observe the reflected image of the initial sphere in the reflection of that sphere! To construct a wild knot, we start with a knot from the catalog; any knot will do except the trivial knot, and we also need a few spherical mirrors, which can be of different sizes. Then, the spheres are strung, one by one, on an imaginary string, making sure that they are sufficiently tight so that the consecutive spheres touch at one point to form a necklace.
The necklace is then knotted according to the diagram of the chosen knot and closed at its ends, making sure that the spheres at the ends also touch each other. A copy of the rest of the necklace is mirrored in each of the spheres of the necklace and these pieces of necklace are connected in consecutive spheres, forming a new necklace made of smaller spheres. This new necklace is more intricate than the previous one, as in each you can see the shape of the knot repeated in each sphere. Moreover, as it is also made of reflecting spheres we can repeat the previous step in this new necklace and so on again, and again into infinity.

The wild knot has infinite details that get smaller and smaller. And, thanks to mathematics, we know that within all these necklaces, there is only one thin curve without ends, infinitely knotted: a wild knot. Indeed, with each step, the spheres reduce in size; and with each step, we add more and more crossings.
Although there are explicit and precise formulas, which, unlike mirrors that show us a flat image on the surface, describe the position of the spheres reflected inside exactly, this idea allows us to imagine wild knots and study them from the point of view of mathematics.
Tu suscripción se está usando en otro dispositivo
¿Quieres añadir otro usuario a tu suscripción?
Si continúas leyendo en este dispositivo, no se podrá leer en el otro.
FlechaTu suscripción se está usando en otro dispositivo y solo puedes acceder a EL PAÍS desde un dispositivo a la vez.
Si quieres compartir tu cuenta, cambia tu suscripción a la modalidad Premium, así podrás añadir otro usuario. Cada uno accederá con su propia cuenta de email, lo que os permitirá personalizar vuestra experiencia en EL PAÍS.
¿Tienes una suscripción de empresa? Accede aquí para contratar más cuentas.
En el caso de no saber quién está usando tu cuenta, te recomendamos cambiar tu contraseña aquí.
Si decides continuar compartiendo tu cuenta, este mensaje se mostrará en tu dispositivo y en el de la otra persona que está usando tu cuenta de forma indefinida, afectando a tu experiencia de lectura. Puedes consultar aquí los términos y condiciones de la suscripción digital.
More information
Últimas noticias
Not all insomnia is the same: Study identifies five subtypes and paves the way for personalized treatment
The United States designates Clan de Golfo as a foreign terrorist group
The United States strikes three more suspected drug boats, killing eight
The Iberian Peninsula is rotating clockwise, scientists report
Most viewed
- ‘El Limones’ and the growing union disguise of Mexican organized crime
- Christian Louboutin: ‘Young people don’t want to be like their parents. And if their parents wear sneakers, they’re going to look for something else’
- ‘We are dying’: Cuba sinks into a health crisis amid medicine shortages and misdiagnosis
- A mountaineer, accused of manslaughter for the death of his partner during a climb: He silenced his phone and refused a helicopter rescue
- Liset Menéndez de la Prida, neuroscientist: ‘It’s not normal to constantly seek pleasure; it’s important to be bored, to be calm’