Grid numbers
EL PAÍS and the Royal Spanish Mathematical Society present their first summer math challenge
In partnership with the Royal Spanish Mathematical Society, EL PAÍS presents its first math challenge of this summer. A new math problem will be published every Thursday until the end of August and readers will have until a minute before midnight on Monday night to send in their answers. Winners will be selected at random from the correct answers and announced on Tuesdays.
Winners will receive the book collection Grandes Ideas de la Ciencia (Great Science Ideas).
The first challenge is set by Adolfo Quirós, who teaches at Madrid’s Autónoma University and is also vice-president of the Royal Spanish Mathematical Society. As well as coming up with this challenge, he has coordinated this whole season of math problems.
Answers must be sent to desafiodeagosto1@gmail.com before 00.00 on Tuesday, August 5 (midnight between Monday and Tuesday). In order to be correct, answers must provide an explanation of how the solution was reached, not just the solution itself.
To try to avoid any mistakes, we will now also explain the challenge in writing, as well as in the above video (in Spanish with English subtitles).
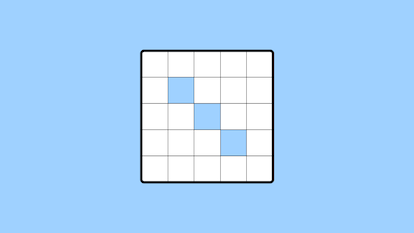
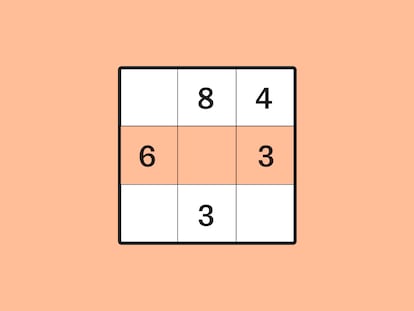
We begin with a four-by-four square grid in which each box contains either the value 1 or the value -1. The game involves changing the numbers around in some of the boxes, following a certain set of rules in order to end up with a 1 value inside every box.
There are two sets of rules to choose from:
- ACB rules (stricter): you may simultaneously change the values of every box in one entire row, one entire column, or one of the two diagonals.
-NBA rules (looser): besides the changes authorized by the ACB rules, you may also simultaneously change all the values in the boxes of an entire line running parallel to one of the two diagonals, which includes the possibility of just changing a corner box value.
We ask you to apply these rules to the two following grids:

For each grid, we ask whether it is possible to succeed in changing all the numbers to a 1 value using each set of rules, and if so, how to do it. The challenge is thus fourfold: for each grid, and using each set of rules, you must explain, in English or Spanish, the steps you used to complete the challenge – or explain why it is not possible to do so.
Tu suscripción se está usando en otro dispositivo
¿Quieres añadir otro usuario a tu suscripción?
Si continúas leyendo en este dispositivo, no se podrá leer en el otro.
FlechaTu suscripción se está usando en otro dispositivo y solo puedes acceder a EL PAÍS desde un dispositivo a la vez.
Si quieres compartir tu cuenta, cambia tu suscripción a la modalidad Premium, así podrás añadir otro usuario. Cada uno accederá con su propia cuenta de email, lo que os permitirá personalizar vuestra experiencia en EL PAÍS.
¿Tienes una suscripción de empresa? Accede aquí para contratar más cuentas.
En el caso de no saber quién está usando tu cuenta, te recomendamos cambiar tu contraseña aquí.
Si decides continuar compartiendo tu cuenta, este mensaje se mostrará en tu dispositivo y en el de la otra persona que está usando tu cuenta de forma indefinida, afectando a tu experiencia de lectura. Puedes consultar aquí los términos y condiciones de la suscripción digital.
Últimas noticias
Aquilino Gonell, former Capitol sergeant: ‘If it hadn’t been for the police, the US would be a dictatorship’
A hybrid building: Soccer pitch, housing, and a shopping mall
Europe urges Trump to respect Greenland following annexation threats
Science seeks keys to human longevity in the genetic mixing of Brazilian supercentenarians
Most viewed
- Alain Aspect, Nobel laureate in physics: ‘Einstein was so smart that he would have had to recognize quantum entanglement’
- Mexico’s missing people crisis casts a shadow over World Cup venue
- Alvin Hellerstein, a 92-year-old judge appointed by Bill Clinton, to preside over Maduro’s trial in New York
- Why oil has been at the center of Venezuela-US conflicts for decades
- Cuba confirms death of 32 of its citizens in the US attack against Venezuela