Grid solution
Lecturer Adolfo Quirós brings us the answer to the first of our summer math challenges
Adolfo Quirós, the vice-president of the Spanish Royal Mathematics Society, lecturer at the Madrid Autonomous University and coordinator of this section, brings us the solution to the first of EL PAÍS’ summer math challenges. The winner of the Grandes Ideas de la Ciencia (or, Major Ideas from Science) collection of books is Guillermo Vicente, an aeronautical engineer from Sabadell who now lives in Torrelodones (Madrid).
To avoid confusion, we have included the solution in written form below.
First let’s consider the ACB rules: the values of all the boxes can be changed in a column, row, or one of the diagonals. Any of these movements will change the sign in four boxes, meaning that if we start with an odd number of -1s, the product will continue to be -1 after any movement. As such we cannot end up with a 1 in all of the boxes in either Grid A nor Grid B.
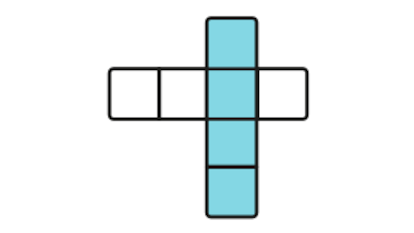
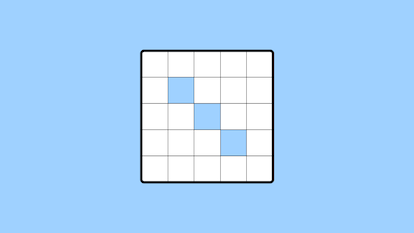
Using the NBA rules, where we can also change the values of all the boxes using a parallel line to the diagonals, the number of changes can be odd or even. In fact, starting with Grid A, you can win in two steps, as indicated by the shaded boxes in this diagram:
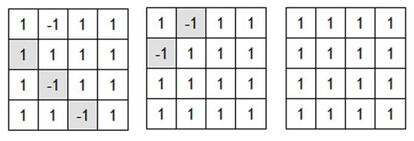
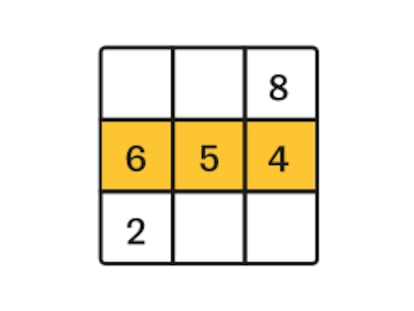
However, if we look at Grid B and the shaded boxes (see the diagram below) we can see that any of the movements allowed by the NBA rules change an even number (none or two) of these boxes. And as there are three -1 you cannot win the game using Grid B.

Tu suscripción se está usando en otro dispositivo
¿Quieres añadir otro usuario a tu suscripción?
Si continúas leyendo en este dispositivo, no se podrá leer en el otro.
FlechaTu suscripción se está usando en otro dispositivo y solo puedes acceder a EL PAÍS desde un dispositivo a la vez.
Si quieres compartir tu cuenta, cambia tu suscripción a la modalidad Premium, así podrás añadir otro usuario. Cada uno accederá con su propia cuenta de email, lo que os permitirá personalizar vuestra experiencia en EL PAÍS.
¿Tienes una suscripción de empresa? Accede aquí para contratar más cuentas.
En el caso de no saber quién está usando tu cuenta, te recomendamos cambiar tu contraseña aquí.
Si decides continuar compartiendo tu cuenta, este mensaje se mostrará en tu dispositivo y en el de la otra persona que está usando tu cuenta de forma indefinida, afectando a tu experiencia de lectura. Puedes consultar aquí los términos y condiciones de la suscripción digital.
Últimas noticias
Trump claims peace in Ukraine is near, but Moscow suggests otherwise
A survivor’s account of the Interoceanic Train accident: ‘We were scared because of the speed on the curve’
The Interoceanic Train, the Mexican alternative to the Panama Canal
What is known about the Interoceanic Train derailment in Oaxaca
Most viewed
- Oona Chaplin: ‘I told James Cameron that I was living in a treehouse and starting a permaculture project with a friend’
- Reinhard Genzel, Nobel laureate in physics: ‘One-minute videos will never give you the truth’
- Why the price of coffee has skyrocketed: from Brazilian plantations to specialty coffee houses
- Pablo Escobar’s hippos: A serious environmental problem, 40 years on
- Chevy Chase, the beloved comedian who was a monster off camera: ‘Not everyone hated him, just the people who’ve worked with him’