A life with pi
Former high-school teacher Manuel Guillera began maths research as therapy But he has since made a major contribution to understanding the mathematical constant
One day in 1913, the British mathematician Godfrey Harold Hardy received a letter from India at his office in Cambridge University. It was signed by an unknown 23-year-old called Srinivasa Ramanujan, who was an accountant in Madras. “I have had no university education but I have undergone the ordinary school course. After leaving school I have been employing the spare time at my disposal to work at mathematics. I have not trodden through the conventional regular course which is followed in a university course, but I am striking out a new path for myself. I have made a special investigation of divergent series in general and the results I get are termed by the local mathematicians as ‘startling’,” wrote Ramanujan.
I was depressed and sought refuge in research. I virtually stopped going out and the only thing that distracted me was work”
The letter was accompanied by reams of paper filled with long, complicated formulas, some of which were to help calculate the infinite decimals of the number pi, which is usually expressed in mathematics as π: 3.1411592653… Hardy later wrote that he had never seen anything like it. “They had to be correct, because nobody would have had the imagination to invent them.”
Ramanujan, using just a pencil and paper, had made mathematical history. Thanks to his theoretical foundations, powerful computers today have calculated the first 10 billion decimals of the number pi.
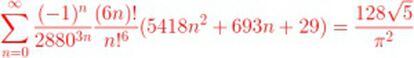
In the late 1990s, almost a century after Ramanujan’s achievements, Jesús Guillera, a high school mathematics teacher from rural Aragón, retired early after his father had died and his mother became ill with Alzheimer’s. “I was depressed and sought refuge in research. I virtually stopped going out and the only thing that distracted me was work. I started looking for things on the internet and came across Ramanujan’s formulas,” he says.
Like his Indian predecessor, Guillera was an outsider who had never studied pi at university. But over many long nights of poring over tables and numbers, he slowly began to develop his own ideas, eventually coming up with a new family of 11 formulas to calculate the number pi, an irrational mathematical constant that follows no pattern over the course of its seemingly infinite figures. “Guillera is our own Ramanujan,” says Javier Cilleruelo, a member of Spain’s Institute of Mathematical Sciences (ICMAT).
In 2002, Guillera summoned up the courage to send an email with his first formulas to a US mathematician
Finally, in 2002, Guillera summoned up the courage to send an email with his first formulas to US mathematician Doron Zeilberger, based at Rutgers University, and internationally regarded as one of the leading lights in pi research. Half-an-hour after looking through Guillera’s work, he replied to the Spaniard, congratulating him on his breakthrough.
“Some mathematicians have compared me to Ramanujan, but there is an important difference: Ramanujan was a genius, and I’m not,” says Guillera. The formulas created by Ramanujan, who died in 1920 at the age of 32, can be explained in the context of ellipses, while the family of formulas developed by Guillera since 2002 are unrelated. The algorithms work, but nobody knows why.

“I think my formulas are very nice, but mathematical beauty is something that is appreciated by mathematicians. You have to see beyond what you are seeing, you have to appreciate what it suggests,” says Guillera. His algorithms work, he says, like “recipes” to which different numbers can be added in infinite series, and from which more and more pi decimals spring. This constant, which has been known for more than 2,000 years, is expressed as the ratio of a circle’s circumference to its diameter. “But in my formulas, there are no circles and no ellipses, which raises the question as to why the number pi appears,” says Guillera, who admits he still does not fully understand his discovery.
If by the age of 15 students don’t like maths, then perhaps it’s better to offer them an alternative”
“It’s a family of formulas from another world, which has nothing to do with ellipses. The question is, where do they come from? Some mathematicians believe they are from the world of the Calabi-Yau, a world that is possibly related to the superstrings,” he says in reference to the theory that everything that exists has emerged from the vibrations of subatomic filaments in a universe of more than four dimensions.
Guillera is critical of the constant changes that have been made by successive Spanish governments to the education system, charging that it has failed children, and that in his final years as a teacher he frequently came across students who even by the age of 13 did not know their multiplication tables. “I found myself teaching at an increasingly basic level,” he says.
It’s a family of formulas from another world, which has nothing to do with ellipses. The question is, where do they come from?”
“If by the age of 15 students don’t like maths, then perhaps it’s better to offer them an alternative, and try to increase their potential in other areas. Not everybody needs to know mathematics. You don’t really need to know much to get by in life,” he says, adding: “If I had been forced to draw from the age of five to 18, and to get good grades, I would hate Cézanne and Renoir today. I don’t know what is the best education system, but the one we have isn’t working.”
Since sending his first formulas to Zeilberger at Rutgers University, Guillera’s work has been published in Proceedings, the journal of the US Mathematics Society, as well as Advances in Applied Mathematics. He has since earned a doctorate in Mathematics at the University of Zaragoza, and regularly gives talks in Spain and abroad, while mathematicians from all over the world continue to try to understand the meaning of his formulas. “I just wish that I had started to do research earlier,” he says.